Source 1
Electron collision studies are fundamental to the understanding of nature, and to many processes in science and industry. These studies provide information on the structure of atoms and molecules, due to the many interactions that occur between them. A complete understanding of these interactions are gained via experiments that allow the development and fine-tuning of theoretical models that predict the behavior of these processes. Such models can then be applied to an array of different uses in science and industry.
Electron collisions with atoms and molecules must be considered carefully due to the many interactions that occur between the incident electron and the atomic or molecular target. These interactions occur prior to, during, and after the collision with the target. The first of these interactions to consider is the long range Coulomb interaction between a single incident electron and an atomic or molecular target as shown in fig. 1.1. This interaction behaves according to Coulomb’s inverse-square law which is a measure of the electrostatic force between charged particles [69].
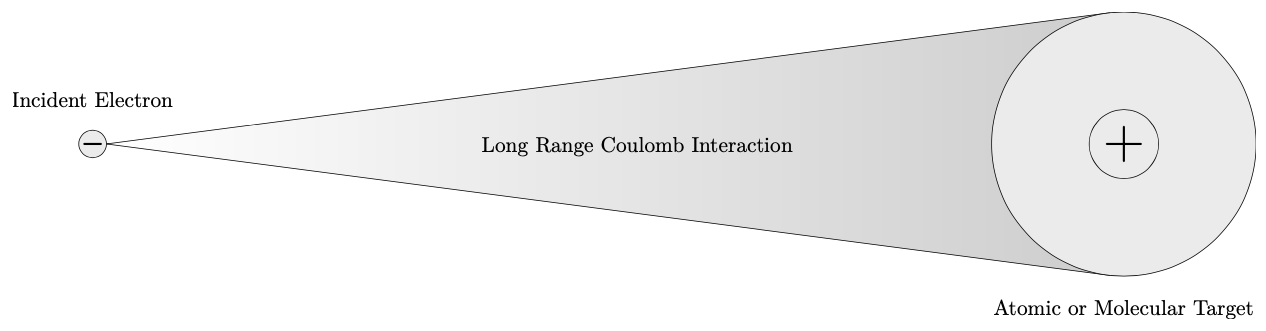
Figure 1.1 The long range Coulomb interaction between an incident electron and an atomic or molecular target. source
The next thing to consider is the time it takes for an electron to interact with an atomic or molecular target. This amount of time is dependent on the energy of the electron. If the incident electron has an energy of 250 eV, then the incident electron is traveling with a non-relativistic velocity of approximately m/s. If the electron is traveling an interaction distance of 100 Å, then the time for the interaction to occur is approximately seconds (or approximately 11 fs). The short interaction times such as the one calculated above, lead to coherent excitation of target states. The energy (and interaction time) an electron travels with can limit the effects of the interactions it encounters prior to, during, and after the collision with an atomic or molecular target. However, the simplest of targets are an n-body problem, with each body exerting its own electrostatic force on other bodies in the system. For this reason the interaction of an electron with an atom or molecule cannot be solved exactly. An example of such an interaction is shown in fig. 1.2, where the incident electron is interacting with the atomic nucleus and its orbiting electrons.
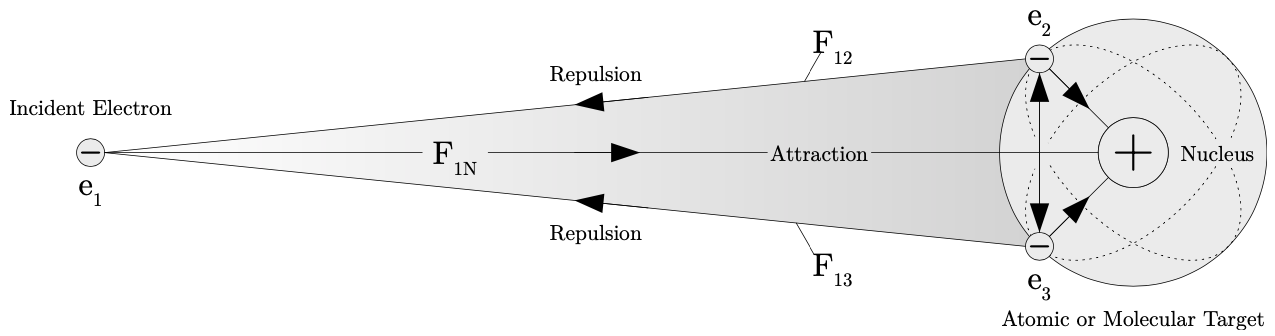
Figure 1.2: An n-body interaction problem where the incident electron 𝑒1 experiences repulsive electrostatic forces and with electrons and respectively. The incident electron experiences an attractive electrostatic force N with the nuclei of the atomic or molecular target. Repulsive electrostatic forces between the bound electrons and , as well as the attractive forces between the bound electrons and the nucleus are indicated by arrows. source
For complex atoms and molecules such as molecular nitrogen and methane where the number of bound (core and valence) electrons are much higher than those shown in fig. 1.2, it becomes more difficult to theoretically solve such n-body problems. For an accurate solution, the theoretical models would have to account for all electron-electron and electron-nuclear interactions. Such a solution is physically impossible to obtain at the present time due to computational and processing limitations. For this reason, many models use approximation methods such as freezing and averaging the core (nucleus and core electrons) and only considering the valence electrons involved in the interactions. In addition to the challenges n-body problems pose, the theoretical models have to take into account processes such as quantum distortions of the electronic wavefunctions, post- collisional Coulomb interactions, multiple collisions, and polarization of the target (as shown in fig. 1.3).
The quantum wave distortions shown in subfigure (a) of fig. 1.3 are the result of the distortion of the initial and final electron Coulomb wavefunctions. The post collisional interactions (PCIs) in subfigure (b) of fig. 1.3 are due to the outgoing electron-electron electrostatic repulsion following collision with and ionization of the atomic or molecular target. In an experiment the outgoing electrons usually cannot be detected at and , because the electron energy analyzers would run into each other at these angles. However, due to post collisional interactions (PCIs), and for electrons having equal energies the electron energy analyzers are not required to reach those angles because the triple differential cross-sections . The multiple scattering shown in subfigure (c) of fig. 1.3 shows a multiple collision of the incident electron with the nucleus then with a valence electron to yield two outgoing electrons. The process shown in subfigure (d) of fig. 1.3 is the polarization of the target due to the Coulomb interaction between the incident electron, the nucleus of the target and its bound electrons [50]. At high energies the effects of some of these interactions and processes are minimized and so can be neglected, thereby making the calculations easier. However, since many of the atomic and molecular spectroscopy experiments (including those detailed in this thesis) are carried out at low to intermediate energies, the contributions by all interactions and quantum processes shown in fig. 1.3 must be equally considered and accounted for in the theoretical models.
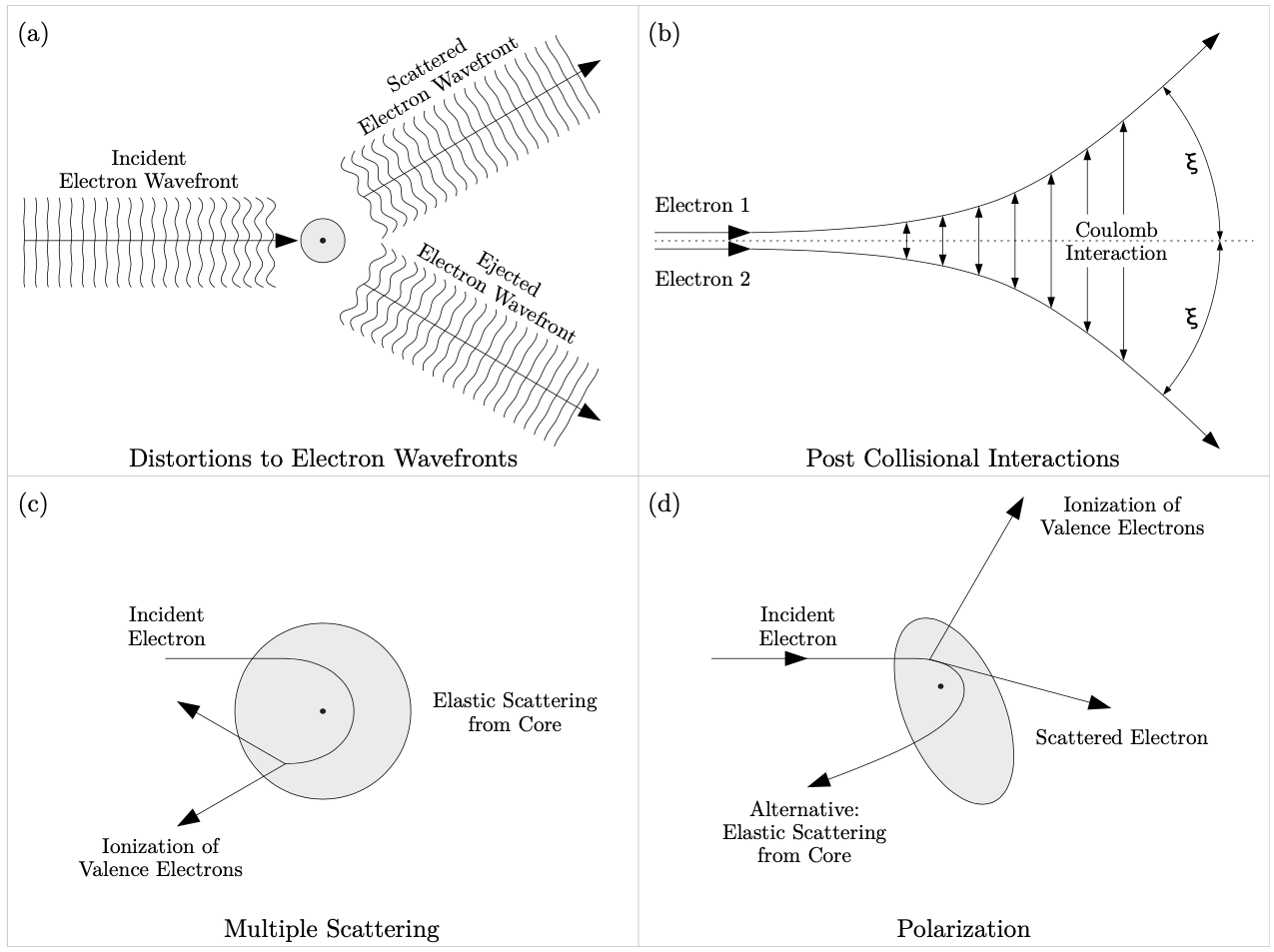
Figure 1.3: Processes of electron collisions. See text for details. source
The electron-atom and electron-molecule interactions in electron impact experiments can produce a variety of scattering types. Electron scattering is the process by which the incident electrons are deviated from their original trajectory due to impact with an atomic or molecular target. Some of the scattering phenomena observed in these experiments are:
Elastic scattering: these are electron collisions where there is no loss of incident energy, but a possible change in momentum of the incident electron upon impact.
Inelastic scattering: these are electron collisions where the incident electron leaves an atomic or molecular target in an excited state.
Ionization: these are electron collisions where the incident electron ionizes the atomic or molecular target, and ejects a valence electron from the target. This process is dependent on the incident energy of the electrons being high enough to ionize the target. Additional ionization processes are ionization with excitation, as well as multiple ionization of the target.
Scattering processes have been fundamental in the discovery and understanding of the structure of atoms. Following the discovery of the electron by J. J. Thomson in 1897 [66], Ernest Rutherford and his colleagues Hans Geiger and Ernest Marsden performed the famous gold foil experiment at the University of Manchester (between 1908 and 1913) [67]. In this experiment a beam of alpha particles were fired at foils of gold. The results of this experiment disproved Thomson’s plum-pudding model of the atom [70], and showed the true structure of the atom; that all of the atom’s positive charge and most of its mass are concentrated in a core called the nucleus.
The gold foil experiment shown in fig. 1.4 was carried out by pointing a beam of alpha particles (helium nuclei) and firing them at a foil of gold that is only a few atoms thick. A fluorescent screen (not shown in fig. 1.4) surrounded the apparatus upon which a scattering pattern emerged following the firing of these alpha particles at the gold atoms. The pattern on the fluorescent screen revealed that the alpha particles scattered in all directions, including the direction back at the alpha particle source. A tiny fraction (around 1 in 8000) of the fired alpha particles were deflected (elastically scattered) by more than 90 degrees. This very scattering pattern was what disproved Thomson’s plum-pudding model of the atom that hypothesized that all alpha particles would have gone straight through and past the gold atoms. These measurements suggested that in order for the alpha particles to scatter in all directions, a strong electrostatic force must have caused some of these deflections to occur, which in turn implied that the atom’s positive charge was densely concentrated in the core of the atom.
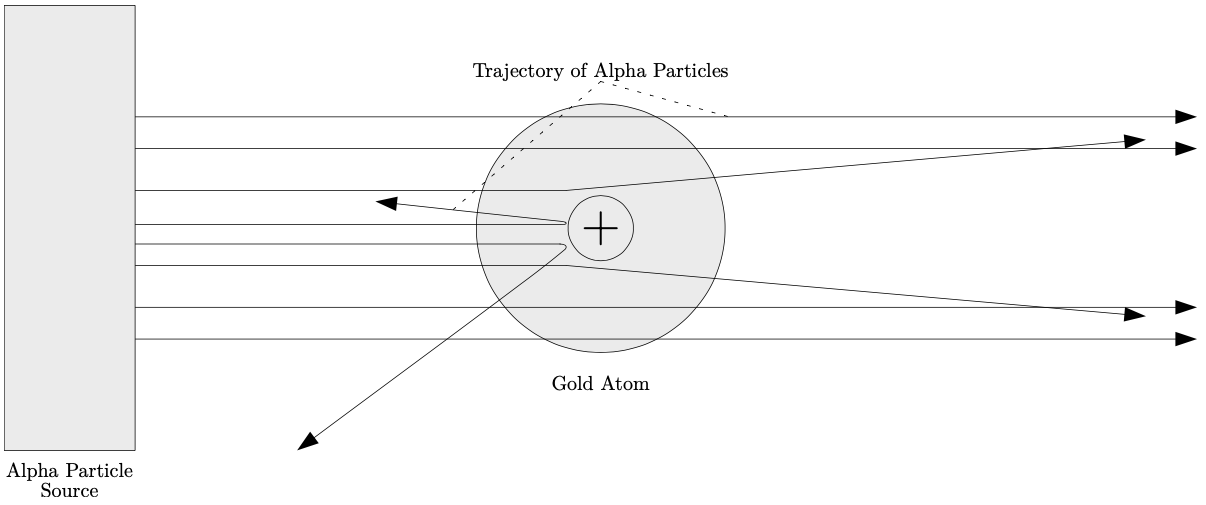
Figure1.4: Rutherford’s gold foil experiment. See text for details. source
These conclusions explained why the positively charged alpha particles were being strongly repelled and deflected the closer they were in their approach towards the nucleus of the gold atom. These conclusions explained why the strength of the repulsive electrostatic force and deflection angle increased with closer distances between an approaching positively charged alpha particle and a nucleus of a gold atom. The small number of alpha particle deflections were explained by the small size of the nucleus. These monumental results led to Rutherford proposing his model for the atom which consisted of mostly empty space, and a cloud of electrons surrounding a dense nucleus where all of the atom’s positive charge was concentrated. The gold foil experiment is a matter-matter interaction and an example of elastic scattering; a process that also occurs in electron collisions with atoms and molecules over all incident electron energies.
PhD Thesis - Ahmad Sakaamini - 2019. ↩︎