Source 1
Ionization by electron impact is a process by which the incident electron travels an interaction distance with an energy sufficient to ionize the target. The result of this interaction are two electrons: the scattering of the incident electron, and the ejection of a valence electron from the atomic or molecular target. Electron impact ionization studies of atoms and molecules are carried out using experiments such as the Manchester (e,2e) coincidence spectrometer.
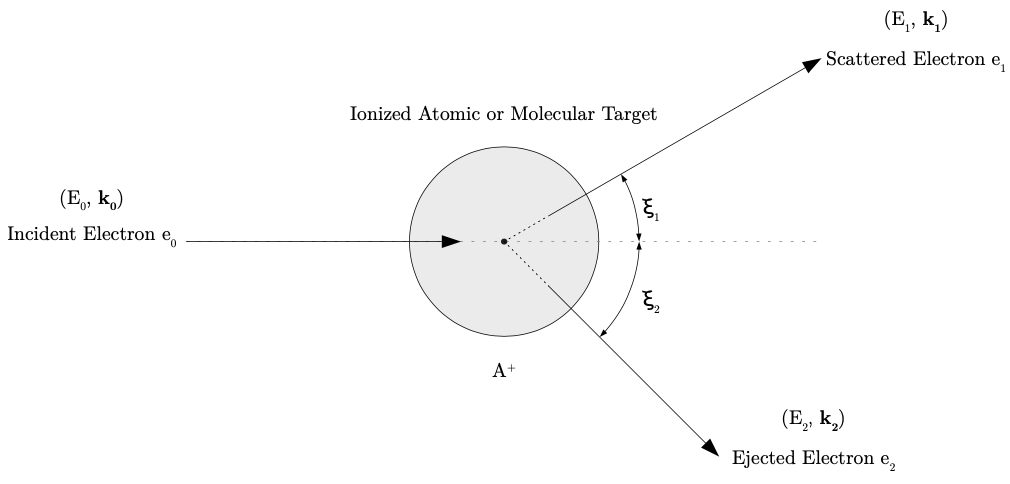
Figure 2.7 The kinematics of ionization by electron impact. source
The kinematics of the ionization process by electron impact is shown in fig. 2.7, where the incident electron travels with an energy and momentum . Upon impact, the atomic or molecular target is ionized and becomes resulting in a scattered (or ejected) electron with energy and momentum , and an ejected (or scattered) electron with energy and momentum . The scattering angles of the outgoing electrons are denoted by and , to distinguish between them and the angles and used to describe the kinematics of the elastic and inelastic scattering processes in the previous sections. The ionization reaction with target can be expressed as:
where
the same is known for the initial and final momenta of the system:
The energies of the initial and final state of the system are
where is the recoil momentum of the target ion and is the mass of the ionized target. The energy of the recoiled ionized atomic or molecular target can be ignored since it is small in comparison to the energy of the incident and outgoing electrons. Electron impact ionization evolves a system from an initial state with one charged particle to a final state with three charged particles, making the entire interaction an n-body problem. In addition, the contributions of the Coulomb interactions and the processes discussed in Electron Collisions play a critical role in determining the exact and final state of the system. The challenges that arise from these complex n-body scattering problems become motivations for the development of sophisticated theoretical models for predicting the behavior of these interactions.
PhD Thesis - Ahmad Sakaamini - 2019. ↩︎